Absolute Maximum Of A Function

Bear witness Mobile Detect Show All NotesHide All Notes

Mobile Notice

You appear to exist on a device with a "narrow" screen width (i.east. you are probably on a mobile telephone). Due to the nature of the mathematics on this site information technology is best views in mural manner. If your device is not in mural mode many of the equations will run off the side of your device (should exist able to curl to meet them) and some of the menu items will be cut off due to the narrow screen width.

Department 4-iii : Minimum and Maximum Values

Many of our applications in this chapter will revolve around minimum and maximum values of a office. While nosotros can all visualize the minimum and maximum values of a function we desire to be a little more specific in our work here. In particular, we want to differentiate between two types of minimum or maximum values. The post-obit definition gives the types of minimums and/or maximums values that we'll be looking at.

Definition

We say that $f\left( x \correct)$ has an absolute (or global) maximum at $ten = c$ if$f\left( x \right) \le f\left( c \right)$ for every $ten$ in the domain we are working on.
We say that $f\left( x \right)$ has a relative (or local) maximum at $ten = c$ if $f\left( x \correct) \le f\left( c \right)$ for every $x$ in some open up interval around $ten = c$.
We say that $f\left( 10 \right)$ has an absolute (or global) minimum at $10 = c$ if $f\left( x \right) \ge f\left( c \correct)$ for every $x$ in the domain we are working on.
We say that $f\left( 10 \right)$ has a relative (or local) minimum at $10 = c$ if$f\left( ten \right) \ge f\left( c \right)$ for every $x$ in some open interval around $ten = c$.

Note that when we say an "open interval effectually$ten = c$" we mean that we can find some interval $\left( {a,b} \right)$, non including the endpoints, such that $a < c < b$. Or, in other words, $c$ will exist contained somewhere inside the interval and will non be either of the endpoints.

Also, we will collectively call the minimum and maximum points of a function the extrema of the function. So, relative extrema will refer to the relative minimums and maximums while absolute extrema refer to the accented minimums and maximums.

Now, let'due south talk a piffling bit nearly the subtle divergence betwixt the accented and relative in the definition above.

We will accept an absolute maximum (or minimum) at $ten = c$ provided $f\left( c \right)$ is the largest (or smallest) value that the part will e'er take on the domain that we are working on. Also, when we say the "domain we are working on" this but means the range of $ten$'s that we have chosen to work with for a given trouble. There may be other values of $x$ that we can actually plug into the function merely have excluded them for some reason.

A relative maximum or minimum is slightly different. All that's required for a bespeak to be a relative maximum or minimum is for that point to be a maximum or minimum in some interval of $x$'s around $ten = c$. In that location may be larger or smaller values of the office at some other identify, but relative to $ten = c$, or local to $10 = c$, $f\left( c \right)$ is larger or smaller than all the other function values that are near information technology.

Note as well that in guild for a point to exist a relative extrema we must be able to expect at function values on both sides of $x = c$ to see if information technology really is a maximum or minimum at that indicate. This means that relative extrema do not occur at the end points of a domain. They tin only occur interior to the domain.

There is really some argue on the preceding indicate. Some folks do feel that relative extrema can occur on the end points of a domain. However, in this course we will be using the definition that says that they can't occur at the end points of a domain. This will exist discussed in a little more detail at the end of the section once we have a relevant fact taken intendance of.

It'south usually easier to get a feel for the definitions by taking a quick expect at a graph.

This is a sketch of some unknown function. The left most point is in the third quadrant and marked as

For the function shown in this graph we take relative maximums at $x = b$ and $ten = d$. Both of these points are relative maximums since they are interior to the domain shown and are the largest bespeak on the graph in some interval around the point. Nosotros also have a relative minimum at $x = c$ since this bespeak is interior to the domain and is the lowest bespeak on the graph in an interval around it. The far-right terminate point, $ten = e$, volition non be a relative minimum since information technology is an finish signal.

The function will have an accented maximum at $10 = d$ and an absolute minimum at $x = a$. These two points are the largest and smallest that the function will ever be. We can also notice that the accented extrema for a office volition occur at either the endpoints of the domain or at relative extrema. We will utilise this thought in afterwards sections and so it's more important than information technology might seem at the nowadays time.

Let'southward take a quick expect at some examples to make sure that nosotros accept the definitions of absolute extrema and relative extrema straight.

Example 1 Identify the absolute extrema and relative extrema for the post-obit function. \[f\left( x \right) = {x^2}\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ { - one,2} \correct]\]

Show Solution

Since this role is piece of cake plenty to graph let's do that. Even so, nosotros only desire the graph on the interval $\left[ { - one,2} \right]$. Here is the graph,

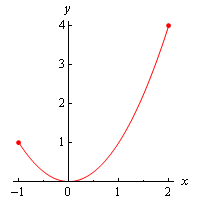
$Graph of $f\left( x \right)={{x}^{2}}$ on the domain $-1 \le x \le 2$ with dots at the (-1,1) and (2,4) to indicate that the graph does not extend past these two points.$

Note that we used dots at the finish of the graph to remind us that the graph ends at these points.

Nosotros can now identify the extrema from the graph. It looks like we've got a relative and absolute minimum of zero at $x = 0$ and an absolute maximum of 4 at $x = ii$. Note that $x = - i$ is non a relative maximum since it is at the finish signal of the interval.

This function doesn't have any relative maximums.

As nosotros saw in the previous instance functions do not accept to have relative extrema. Information technology is completely possible for a function to non have a relative maximum and/or a relative minimum.

Instance 2 Place the absolute extrema and relative extrema for the following function. \[f\left( ten \right) = {x^2}\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ { - 2,2} \correct]\]

Show Solution

Here is the graph for this function.

$Graph of $f\left( x \right)={{x}^{2}}$ on the domain $-2 \le x \le 2$ with dots at the (-2,4) and (2,4) to indicate that the graph does not extend past these two points.$

In this case we even so have a relative and absolute minimum of cypher at $x = 0$. We also still accept an absolute maximum of four. However, dissimilar the first case this will occur at 2 points, $ten = - 2$ and $ten = 2$.

Once again, the function doesn't take any relative maximums.

As this example has shown there tin only be a single accented maximum or accented minimum value, but they tin occur at more than one place in the domain.

Example 3 Identify the absolute extrema and relative extrema for the following part. \[f\left( ten \right) = {ten^2}\]

Prove Solution

In this case we've given no domain and and so the assumption is that we volition accept the largest possible domain. For this office that ways all the existent numbers. Here is the graph.

$Graph of $f\left( x \right)={{x}^{2}}$ with no domain specified and arrows at the ends pointing upwards to indicate the graph continues.$

In this example the graph doesn't finish increasing at either end and so at that place are no maximums of whatever kind for this function. No thing which point nosotros choice on the graph there will be points both larger and smaller than it on either side so we can't take whatsoever maximums (of any kind, relative or absolute) in a graph.

We still have a relative and absolute minimum value of zip at $x = 0$.

And so, some graphs can have minimums but not maximums. Likewise, a graph could have maximums but not minimums.

Example 4 Identify the absolute extrema and relative extrema for the post-obit function. \[f\left( x \correct) = {ten^three}\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ { - 2,2} \right]\]

Show Solution

Here is the graph for this function.

$Graph of $f\left( x \right)={{x}^{3}}$ on the domain $-2 \le x \le 2$ with dots at the (-2,-8) and (2,8) to indicate that the graph does not extend past these two points.$

This part has an absolute maximum of eight at $10 = 2$ and an absolute minimum of negative 8 at $x = - 2$. This function has no relative extrema.

And then, a function doesn't take to have relative extrema as this example has shown.

Example 5 Identify the absolute extrema and relative extrema for the following part. \[f\left( x \correct) = {x^iii}\]

Show Solution

Again, we aren't restricting the domain this time so hither's the graph.

$Graph of $f\left( x \right)={{x}^{3}}$ with no domain specified and arrows at the ends to indicate the graph continues.$

In this example the part has no relative extrema and no absolute extrema.

Every bit we've seen in the previous example functions don't have to have any kind of extrema, relative or absolute.

Example 6 Identify the absolute extrema and relative extrema for the following function. \[f\left( ten \correct) = \cos \left( x \right)\]

Evidence Solution

We've not restricted the domain for this function. Here is the graph.

$Graph of $f\left( x \right)=\cos \left( x \right)$ on the domain $\left[ -3\pi ,3\pi \right]$ and arrows at the ends to indicate the graph continues.$

Cosine has extrema (relative and accented) that occur at many points. Cosine has both relative and accented maximums of 1 at

\[x = \ldots - four\pi ,\, - ii\pi ,\,\,0,\,\,2\pi ,\,\,4\pi , \ldots \]

Cosine also has both relative and absolute minimums of -1 at

\[ten = \ldots - 3\pi ,\, - \pi ,\,\,\pi ,\,\,iii\pi , \ldots \]

As this case has shown a graph can in fact have extrema occurring at a large number (infinite in this example) of points.

We've now worked quite a few examples and we tin can use these examples to see a nice fact about accented extrema. First let'south find that all the functions above were continuous functions. Side by side discover that every fourth dimension we restricted the domain to a airtight interval (i.e. the interval contains its end points) nosotros got absolute maximums and accented minimums. Finally, in only one of the three examples in which we did not restrict the domain did we become both an absolute maximum and an absolute minimum.

These observations atomic number 82 us the following theorem.

Extreme Value Theorem

Suppose that $f\left( ten \right)$ is continuous on the interval $\left[ {a,b} \right]$ and so at that place are two numbers $a \le c,d \le b$ so that $f\left( c \correct)$ is an absolute maximum for the function and $f\left( d \right)$ is an absolute minimum for the part.

So, if we take a continuous role on an interval $\left[ {a,b} \right]$ then we are guaranteed to take both an absolute maximum and an absolute minimum for the function somewhere in the interval. The theorem doesn't tell us where they will occur or if they will occur more than once, but at to the lowest degree it tells united states of america that they practise exist somewhere. Sometimes, all that we need to know is that they do exist.

This theorem doesn't say anything most absolute extrema if nosotros aren't working on an interval. Nosotros saw examples of functions above that had both absolute extrema, one accented extrema, and no accented extrema when nosotros didn't restrict ourselves down to an interval.

The requirement that a function exist continuous is likewise required in order for us to use the theorem. Consider the case of

\[f\left( x \right) = \frac{ane}{{{x^2}}}\hspace{0.25in}{\mbox{on}}\hspace{0.25in}[ - ane,1]\]

Here'southward the graph.

$Graph of $f\left( x \right)=\frac{1}{{{x}^{2}}}$ on the domain $-1 \le x \le 1$ with dots at the (-1,1) and (1,1) to indicate that the graph does not extend past these two points. There is also a gap as the graph approaches the y-axis to indicate that the graph will continue to move up the y-axis as it approaches.$

This office is non continuous at $ten = 0$ as we move in towards zilch the function is budgeted infinity. So, the function does not have an absolute maximum. Notation that it does have an absolute minimum however. In fact the accented minimum occurs twice at both $x = - i$ and $x = i$.

If we changed the interval a piffling to say,

\[f\left( ten \right) = \frac{1}{{{x^2}}}\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ {\frac{1}{2},ane} \right]\]

the function would at present take both accented extrema. We may only run into problems if the interval contains the point of discontinuity. If it doesn't then the theorem volition hold.

We should also signal out that but because a function is non continuous at a point that doesn't hateful that it won't have both accented extrema in an interval that contains that point. Below is the graph of a function that is not continuous at a point in the given interval and even so has both absolute extrema.

This is the graph of some unknown function. The left most point is in the third quadrant and labeled

This graph is non continuous at $x = c$, nevertheless it does have both an absolute maximum ($x = b$) and an absolute minimum ($ten = c$). Too notation that, in this example one of the absolute extrema occurred at the bespeak of discontinuity, but it doesn't need to. The absolute minimum could simply take easily been at the other end point or at another point interior to the region. The betoken hither is that this graph is not continuous and nevertheless does have both absolute extrema

The point of all this is that we need to be conscientious to only apply the Extreme Value Theorem when the weather of the theorem are met and non misinterpret the results if the weather condition aren't met.

In order to utilise the Extreme Value Theorem nosotros must take an interval that includes its endpoints, frequently called a closed interval, and the role must be continuous on that interval. If we don't have a airtight interval and/or the role isn't continuous on the interval then the function may or may not accept absolute extrema.

We demand to discuss 1 final topic in this section before moving on to the first major awarding of the derivative that we're going to be looking at in this affiliate.

Fermat's Theorem

If $f\left( x \right)$ has a relative extrema at $x = c$ and $f'\left( c \right)$ exists then $x = c$ is a critical bespeak of $f\left( x \correct)$. In fact, information technology volition be a critical point such that $f'\left( c \right) = 0$.

To meet the proof of this theorem run into the Proofs From Derivative Applications department of the Extras affiliate.

Also note that nosotros can say that $f'\left( c \right) = 0$ because we are also assuming that $f'\left( c \right)$ exists.

This theorem tells united states that there is a overnice relationship between relative extrema and disquisitional points. In fact, it will permit u.s.a. to get a list of all possible relative extrema. Since a relative extrema must be a critical betoken the list of all disquisitional points will give us a list of all possible relative extrema.

Consider the case of $f\left( x \right) = {10^2}$. We saw that this office had a relative minimum at $x = 0$ in several earlier examples. So co-ordinate to Fermat's theorem $10 = 0$ should be a critical betoken. The derivative of the function is,

\[f'\left( ten \right) = 2x\]

Sure enough $x = 0$ is a critical signal.

Be careful non to misuse this theorem. It doesn't say that a critical point will exist a relative extrema. To run into this, consider the following case.

\[f\left( x \correct) = {x^iii}\hspace{0.25in}\hspace{0.25in}f'\left( ten \correct) = 3{x^2}\]

Clearly $x = 0$ is a disquisitional bespeak. Yet, we saw in an earlier case this role has no relative extrema of whatsoever kind. And so, critical points do not have to be relative extrema.

Also note that this theorem says naught about absolute extrema. An accented extrema may or may not be a critical point.

Before we leave this section nosotros need to discuss a couple of issues.

Showtime, Fermat's Theorem only works for disquisitional points in which $f'\left( c \right) = 0$. This does not, nonetheless, hateful that relative extrema won't occur at disquisitional points where the derivative does not exist. To come across this consider $f\left( x \right) = \left| x \correct|$. This function clearly has a relative minimum at $x = 0$ and yet in a previous department we showed in an example that $f'\left( 0 \correct)$ does not be.

What this all means is that if we want to locate relative extrema all nosotros really need to do is look at the critical points as those are the places where relative extrema may exist.

Finally, remember that at that start of the department nosotros stated that relative extrema will not exist at endpoints of the interval we are looking at. The reason for this is that if we allowed relative extrema to occur at that place it may well (and in fact near of the time) violate Fermat's Theorem. There is no reason to await end points of intervals to be critical points of whatever kind. Therefore, we practise non let relative extrema to be at the endpoints of intervals.